Directives sur l’environnement physique extracôtier
Annexe A – Vérification des prévisions
A.1 Tour d'horizon
A.2 Paramètres de vérification recommandés
A.3 Observations
A.4 Prévisions
A.5 Graphiques chronologiques
A.6 Statistiques de vérification
A.6.1 Erreur
A.6.2 Erreur systématique
A.6.3 Erreur absolue moyenne
A.6.4 Erreur quadratique moyenne
A.6.5 Indice de comparaison
A.7 Analyse des valeurs limites
A.7.1 Pourcentage d'exactitude
A.7.2 Probabilité de repérage
A.7.3 Taux de fausses alarmes
A.4.4 Taux d'événements ratés
A.1 - Tour d'horizon
La vérification des prévisions permet aux exploitants extracôtiers d'effectuer des comparaisons et d'évaluer la fiabilité du programme de prévisions. Un bon degré de certitude des prévisions permettra à l'exploitant de s'en servir pour orienter ses décisions opérationnelles.
De manière à produire des prévisions et des statistiques de vérification fiables, il incombe à l'exploitant de donner accès, à l'entrepreneur en prévisions, à des observations précises et en temps opportun.
Les statistiques de vérification servent à mesurer le degré de correspondance entre prévisions et observations. Par conséquent, il s'agit d'une indication de l'efficacité conjointe des programmes d'observations et de prévisions. Les renseignements de vérification devraient être mis à jour et présentés aux utilisateurs des prévisions le plus rapidement possible.
Les principaux objectifs de la vérification des prévisions sont les suivants :
- l'évaluation du degré d'exactitude des prévisions;
- l'évaluation du degré d'exactitude et de représentativité des observations;
- l'examen des tendances dans les prévisions en vue de l'amélioration de leur qualité;
- une connaissance accrue de l'incidence de l'information et des conditions météorologiques sur les activités extracôtières dans le but d'en évaluer les risques.
Il est recommandé qu'une analyse de vérification des prévisions, semblable à celle présentée dans la présente annexe, fasse partie intégrante du programme de prévisions.
A.2 Paramètres de vérification recommandés
Les paramètres ayant une incidence de premier plan sur les activités maritimes extracôtières sont la vitesse et la direction du vent ainsi que la hauteur des vagues. Il est recommandé de vérifier au moins ces paramètres dans le cadre de tous les programmes de prévisions. Lorsque des prévisions tactiques des glaces sont requises, les positions prévues des glaces ou des icebergs devraient également être vérifiées. D'autres paramètres, comme la température de l'air et la visibilité, peuvent mériter d'être pris en considération selon leur importance pour l'activité visée.
Il incombe à l'exploitant d'établir les paramètres de prévision à vérifier.
A.3 Observations
Une valeur d'observation utilisée à des fins de vérification devrait se rapprocher le plus possible de la définition du paramètre de prévision correspondant (voir la section qui suit). Une telle correspondance peut être difficile à obtenir en raison des limites afférentes aux observations découlant, au nombre d'autres facteurs, d'un emplacement des instruments qui pourrait être meilleur. Les obstructions, notamment attribuables à la superstructure de l'installation et aux effets thermiques, peuvent empêcher les instruments d'enregistrer les conditions ambiantes.
Par exemple, il peut falloir :
- éliminer toute erreur systématique des observations - dans le cas des observations du vent, il peut exister des erreurs d'observation à la fois de la vitesse et de la direction du vent qui doivent être éliminées avant d'utiliser ces observations dans une analyse;
- appliquer toute moyenne spatiale ou temporelle de façon que les définitions des observations équivalent aux paramètres de prévision correspondants;
- effectuer tous les ajustements requis de manière que les observations et les prévisions fassent référence à une même hauteur au-dessus du niveau de la mer;
- tenir compte, au besoin, de toute dérive physique - par exemple, il faudrait vérifier les prévisions d'humidité en ayant recours aux mesures du thermomètre sec et du thermomètre mouillé.
De plus, les observations incluses dans le système de vérification doivent correspondre à la définition des paramètres de prévision à vérifier (voir la section qui suit). Par exemple, la formule suivante peut servir à traiter des observations utilisées dans un système de vérification.
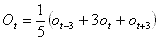 Équation 1
Équation 1
Dans cette formule, ot représente les vents observés pour le temps valable t, 3 heures avant ce temps et 3 heures après. Les observations des vents maritimes (c.-à-d. les vents dans le MANMAR [5]) peuvent par exemple être traitées en se servant de l'équation 1. On aurait recours à différentes expressions si des observations pour l'aviation ou des « valeurs obtenues au moyen de capteurs » étaient utilisées à l'intérieur du système de vérification.
A.4 Prévisions
Des définitions précises des paramètres des prévisions à vérifier sont requises. En ce sens, les éléments suivants doivent être définis pour chacun des paramètres des prévisions :
- l'aire spatiale horizontale et verticale qui s'applique;
- la hauteur de référence verticale;
- le degré de représentativité temporelle;
- l'intervalle de calcul des moyennes (d'échantillonnage).
Par exemple, les prévisions des vents moyens sur 10 minutes valables pour un anémomètre situé à une hauteur de 60 mètres peuvent être vérifiées. Les vents prévus peuvent représenter une période de 6 heures autour du temps valable pour les prévisions selon la formule suivante de calcul des moyennes.
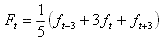 Équation 2
Équation 2
Dans cette formule, ft représente les vents moyens sur 10 minutes pour le temps valable t, 3 heures avant ce temps et 3 heures après. La définition des paramètres des prévisions devrait être bien connue par tous les utilisateurs des prévisions.
A.5 Graphiques chronologiques
Un ensemble de graphiques chronologiques mensuels des prévisions et paramètres observés constitue une composante de vérification recommandée. Tel que mentionné à la section E.3, tous les calculs requis afin que les observations et les prévisions correspondent entre elles doivent être effectués avant de tracer les graphiques. Des graphiques pour des délais de prévision de 12, 24, 36 et 48 heures peuvent être tracés. Aux fins de vérification, les délais doivent être établis en fonction de la date/de l'heure de la plus récente analyse synoptique effectuée sur laquelle sont fondées les prévisions. Par exemple, à des prévisions produites à 240700 UTC en fonction d'une analyse synoptique effectuée à 240000 UTC sera associé un temps de validation de 36 heures à 251200 UTC. Des axes verticaux et temporels cohérents devraient être utilisés. Il est utile de tenir compte des valeurs limites opérationnelles éventuelles au moment du tracé des graphiques chronologiques.
A.6 Statistiques de vérification
Le recours à un ensemble de statistiques de vérification est recommandé. Les statistiques suivantes sont décrites en détail ci-après :
- Erreur
- Erreur systématique
- Erreur absolue moyenne
- Erreur quadratique moyenne
- Indice de comparaison
A.6.1 Erreurr
La différence entre la prévision et l'observation, à un temps donné t, est obtenue comme suit :
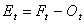 Équation 3
Équation 3
L'erreur de prévision est obtenue comme suit :
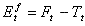 Équation 4
Équation 4
L'erreur d'observation est obtenue comme suit :
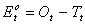 Équation 5
Équation 5
Dans les formules qui précèdent, Tt représente la « valeur véritable », soit la valeur qui serait mesurée au moyen d'un instrument non biaisé (c.-à-d. parfait). Dans les définitions qui précèdent, l'erreur respecte la formule qui suit :
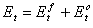 Équation 6
Équation 6
C'est dire que la prévision et l'observation comportent toutes deux une composante d'erreur. Si possible, les erreurs d'observation devraient être éliminées avant d'utiliser les observations dans un système de vérification. Autrement, les statistiques de vérification reflètent indûment des erreurs tant dans les programmes d'observation que dans les programmes de prévision. L'évaluation des erreurs d'observation est une marche à suivre pour l'assurance de la qualité du programme d'observation.
A.6.2 Erreur systématique
L'erreur systématique est obtenue comme suit :
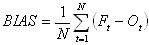 Équation 7
Équation 7
L'erreur systématique indique l'écart moyen entre les prévisions et les observations. Il peut s'agir d'une valeur négative ou positive. L'erreur systématique mesure la « direction » (c.-à-d. positive ou négative) mais non l'ampleur des erreurs et sa valeur devrait se situer aux alentours de zéro.
A.6.3 Erreur absolue moyenne
L'erreur absolue moyenne est obtenue comme suit :
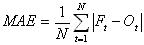 Équation 8
Équation 8
Cette statistique mesure l'ampleur moyenne des erreurs, sans toutefois en indiquer la direction. L'erreur absolue moyenne est toujours positive et inférieure ou égale à l'erreur quadratique moyenne.
A.6.4 Erreur quadratique moyenne
L'erreur quadratique moyenne est obtenue comme suit :
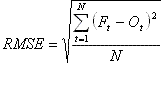 Équation 9
Équation 9
Cette statistique mesure également l'ampleur moyenne des erreurs et elle n'en indique pas elle non plus la direction. Comparativement à l'erreur absolue moyenne, l'erreur quadratique moyenne accorde davantage de poids aux erreurs d'envergure qu'aux autres au moment du calcul de la moyenne. Ainsi, lorsque l'erreur quadratique moyenne est de beaucoup supérieure à l'erreur absolue moyenne, cela signifie une fréquence accrue d'erreurs d'envergure. Il s'agit donc d'une statistique appropriée lorsque des erreurs d'envergure sont très peu souhaitables. Cette statistique évite les « écarts importants » alors qu'un spécialiste des prévisions peut comprimer l'erreur quadratique moyenne au moyen de prévisions qui se situent à mi-chemin des prévisions possibles (c.-à-d. en évitant les prévisions de valeurs extrêmes).
A.6.5 Indice de comparaison
L'indice de comparaison est obtenu comme suit :
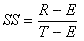 Équation 10
Équation 10
Dans la formule qui précède :
| R | représente le nombre de prévisions exactes; |
| T | représente le nombre total de prévisions; |
| E | représente le nombre prévu de prévisions exactes fondées sur les valeurs climatologiques d'une zone précise en fonction de données de reconstitution sur les vagues et le vent (pas exemple, données de reconstitution AES40 [13]) de la zone extracôtière locale. |
Il faut savoir que :
| SS | = 1 lorsque toutes les prévisions sont exactes; |
| = 0 lorsque le nombre de prévisions exactes est identique à celui attendu; | |
| = une valeur négative en présence de prévisions qui produisent plus d'inexactitudes que prévu au moment de la comparaison avec le climat local connu. |
Ainsi défini, l'indice de comparaison exprime sous forme de fraction décimale le pourcentage des prévisions exactes après élimination de celles qui auraient été exactes en se fondant sur la connaissance du climat local.
Les caractéristiques de l'indice de comparaison sont les suivantes :
- L'éventail des valeurs possibles de l'indice de comparaison va de +1 à moins l'infini, cette dernière valeur étant mathématiquement possible avec des prévisions normalisées parfaites (E=T et E>R), indépendamment du degré de précision des prévisions véritables (seules restriction : E>R).
- Plus grande est la normalisation des données climatologiques, plus faible sera l'indice de comparaison pour un ensemble précis de prévisions. En outre, plus petit est l'ensemble de prévisions, plus importante est la probabilité d'une normalisation qui sera, accidentellement, très bonne et difficile à surpasser.
- Lorsque deux techniques de prévisions éprouvées différentes sont appliquées à un ensemble représentatif de données, celle des deux qui produit l'indice positif le plus élevé sera la plus utile.
- L'indice de comparaison constitue un bon paramètre de comparaison des prévisions de différentes régions climatiques.
- L'indice de comparaison est d'abord et avant tout une note de synthèse.
Pour résumer, l'indice de comparaison varie en fonction des données climatologiques servant aux calculs. Cependant, il s'agit d'un indicateur important pour l'évaluation de l'exactitude des prévisions. Une note entre 0 et 1 indique la présence de bonnes prévisions dans le contexte de la climatologie.
A.7 Analyse des valeurs limites
Des valeurs limites sont définies en vue d'établir les exigences opérationnelles. En général, l'exploitant souhaite connaître le degré de précision des prévisions en tenant compte de valeurs limites opérationnelles convenues d'avance. Les valeurs limites pour la vitesse du vent et la hauteur des vagues devraient tenir compte de la zone d'exploitation, du type d'installations et de la nature des activités critiques. C'est en collaboration avec l'entrepreneur que l'exploitant devrait choisir les valeurs limites qui serviront à la vérification des prévisions.
Pour obtenir des résultats significatifs, une analyse des valeurs limites devrait porter sur une période raisonnable qui sera témoin d'un nombre suffisant de situations de dépassement de ces valeurs. Dans le cas de travaux de forage ou de programmes de production de longue durée, les statistiques devraient être calculées pour chaque saison, tandis que s'il s'agit de programmes de forage de moindre portée (entre 1 et 4 mois), la durée complète des travaux de forage ou du programme de production pourrait constituer une période plus raisonnable pour les calculs.
Dans le contexte de l'analyse des valeurs limites, les prévisions et les valeurs observées appartiennent à l'une ou l'autre des quatre catégories suivantes :
- la prévision prédit correctement que la valeur limite sera dépassée;
- la prévision prédit correctement que la valeur limite ne sera pas dépassée;
- la prévision prédit incorrectement que la valeur limite sera dépassée (fausse alarme);
- la prévision prédit incorrectement que la valeur limite ne sera pas dépassée (événement raté).
La probabilité de repérage, le taux de fausses alarmes et le taux d'événements ratés sont obtenus à partir d'un tableau de contingence (tableau A-1). Il s'agit d'atteindre la probabilité de repérage la plus élevée possible tout en maintenant le plus bas possible les taux d'événements ratés et de fausses alarmes. Les fausses alarmes entraînent des coûts inutiles tandis que les événements ratés ont des répercussions tant à l'égard des coûts qu'en matière de sécurité.
Le tableau de contingence des valeurs limites suit.
Tableau A-1 - Tableau de contingence pour l'analyse des valeurs limites
| Prévisions (f) | ||||
|---|---|---|---|---|
| Dépassement des valeurs limites | Non dépassement des valeurs limites | Totaux | ||
| Observations (o) |
Dépassement des valeurs limites |
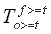 |
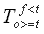 |
No>=t |
| Non dépassement des valeurs limites |
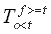 |
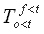 |
No<t | |
| Totaux | Nf>=t | Nf<t | Ntotal | |
Dans le tableau qui précède :
| o | = Valeur observée; |
| f | = Valeur prévue; |
| t | = Valeur limite; |
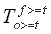 |
= Nombre de fois que la valeur observée dépasse la valeur limite et que la valeur prévue dépasse la valeur limite; |
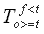 |
= Nombre de fois que la valeur observée dépasse la valeur limite et que la valeur prévue ne dépasse pas la valeur limite; |
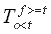 |
= Nombre de fois que la valeur observée ne dépasse pas la valeur limite et que la valeur prévue dépasse la valeur limite; |
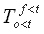 |
= Nombre de fois que la valeur observée ne dépasse pas la valeur limite et que la valeur prévue ne dépasse pas la valeur limite; |
| Nf>=t | = Nombre de fois que la prévision dépasse la valeur limite (et ainsi de suite avec les autres totaux). |
Des statistiques utiles pour la vérification des valeurs limites sont décrites ci-après.
A.7.1 Pourcentage d'exactitude
Le pourcentage d'exactitude est obtenu comme suit :
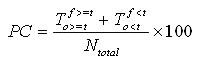 Équation 11
Équation 11
Cette statistique peut varier de 0 à 100.
A.7.2 Probabilité de repérage
La probabilité de repérage mesure la capacité du programme de prévisions à prédire avec succès les événements où « les valeurs limites sont dépassées ».
La probabilité de repérage est obtenue comme suit :
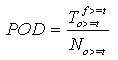 Équation 12
Équation 12
Cette statistique peut varier de 0 à 1.
A.7.3 Taux de fausses alarmes
Le taux de fausses alarmes mesure les prévisions incorrectes d'événements où « les valeurs limites sont dépassées ».
Le taux de fausses alarmes est obtenu comme suit :
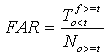 Équation 13
Équation 13
Cette statistique peut varier de 0 à 1.
A.7.4 Taux d'événements ratés
Le taux d'événements ratés mesure les prévisions incorrectes d'événements où « les valeurs limites ne sont pas dépassées ».
Le taux d'événements ratés est obtenu comme suit :
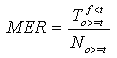 Équation 14
Équation 14
Cette statistique peut varier de 0 à 1.
- Date de modification :
